Calculating the Volume of Concrete in Slab, Beam, Column, Retaining wall, & Footing

Volume is a measure of how much space occupies. Consider a glass filled with water. The volume of water in the glass is the water that occupies the space within the glass.

The same thing applies to concrete. Three dimensions are multiplied to calculate volume, so it is the calculation of three dimensions.

Procedure

The volume of concrete must be worked out first, and then the quantities of the individual ingredients must be calculated.

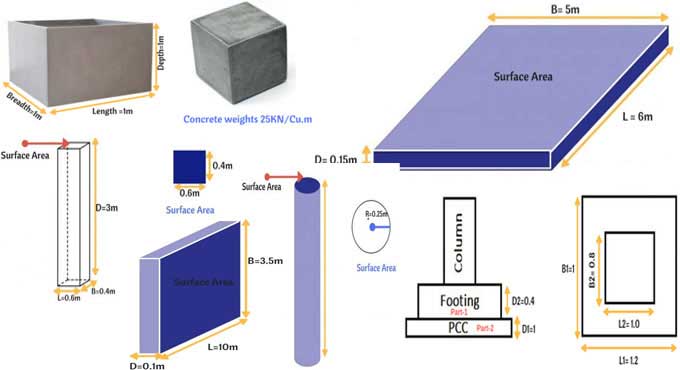
? Fill a box of length 1metre, width 1metre, depth 1metre with concrete.
? 1 meter x 1 meter x 1 meter = 1 m3 of concrete.
? 25KN of concrete is needed to fill 1m3 of the box, where 1KN = 100Kg.

The formula changes depending on the shape, but the methodology remains the same, namely multiplying the three dimensions to calculate the volume of any shape. Imagine a cylinder that does not have a length and a width. A cylinder's volume is calculated by multiplying its surface area by its height.

Volume of Concrete Calculation

Column

Columns may be rectangular, circular, hexagonal or any other shape. It is calculated by multiplying the surface area by the depth.

Circular Column

Circle radius = 0.25 m.
A circular column's volume is calculated by multiplying its surface area by its height.
A circular column has a volume equal to 3.14 x 0.252 x 3 = 0.58m3.

Rectangular Column

The length of the column is 0.6m, the width is 0.4m, and the height of the column is 3m
A surface area is calculated by multiplying the column's height and depth.
Concrete volume: 0.6?0.4?3= 0.72m3.

Beam

The top or bottom surface area of a beam is multiplied by the beam's depth to determine how much concrete is needed for beams. A rectangular beam equals 4x0.5x0.4=0.8m3 of concrete after adding surface area and depth.

Retaining Wall

It is roughly the same for retaining walls as it is for slabs, but the amount of material used is not changed. Concrete volume in retaining walls is calculated by multiplying surface area by depth is the same as 10?3.5?0.1 =3.5m3.

Footing

A. The building has dimensions of 1.0m by 0.8m by 0.4m in a rectangular shape.
B. 1.0m*0.8*0.4 = 0.32m3 volume of 2nd part.
C. Concrete volume = 1.2 x 1 x 0.1 = 0.12 m3.
D. A total of 0.32m3 plus 0.12m3 = 0.44m3 of concrete for a footing.

Calculation of Volume of Material

1. The density of cement is 1440 kg/cubic meter approximate.

2. One kilogram of cement is equal to 1/1440, or 0.000694 kilograms.

3. Cement from one bag 50 kg contains 0.035 cubic meters.

4. Taking into account the cement to sand (1:2) and cement to aggregate (1:4) ratios.

5. The required amount of Sand would be 0.035*2 = 0.07 cubic meters.

6. Assuming 0.035 cubic meters of aggregate is required per lane that equals 0.14 cubic meters.

Wrapping it Up

There are different types of concrete structures based on what they are used for. It is possible to calculate the amount of concrete required by adding up the volumes of each structural member.

It is possible to calculate the volume of a rectangular cross-sectional member by multiplying the length by the width by the height or the depth by the thickness. The appropriate formula must be used to determine the cross-sectional shape of different members.

To learn more, watch the following video tutorial.

Video Source: Civil Engineer Deepak Kumar