Designing and detailing of Reinforced Concrete Structures

What is Reinforced Concrete
Reinforced concrete (RC) is a versatile composite and one of the most widely used materials in modern construction. Concrete is a relatively brittle material that is strong under compression but less so in tension. Plain, unreinforced concrete is unsuitable for many structures as it is relatively poor at withstanding stresses induced by vibrations, wind loading, and so on.
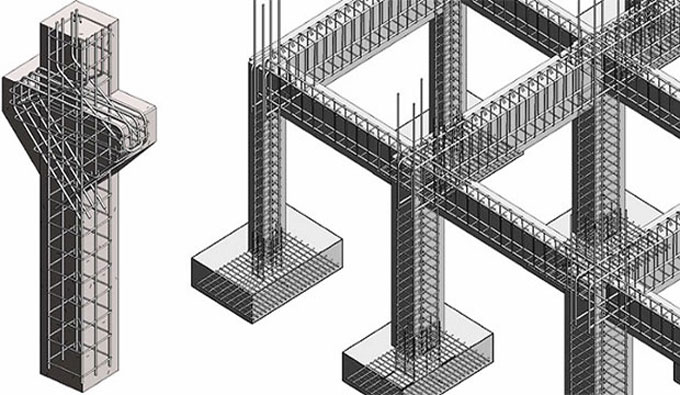
Benefits in detailing in Concrete Structures
Detailing involves the communication of the engineer?s design to the contractors who build the structure. Good detailing ensures that reinforcement and concrete interact efficiently to provide satisfactory behaviour throughout complete range of loading.
There are many benefits if we apply good detailing to reinforced Concrete structures, some of them are mentioned below:
1. Detailing is very important not only for the proper execution of the structures but for the safety of the structures.
2. A design engineer's responsibility should include assuring the structural safety of the design, details, checking shop drawing.
3. Detailing is necessary not only for the steel structures as well as reinforced concrete structures as it is the translation of all the mathematical expression's and equation's results.
Methods used in Designing Reinforced Concrete Structures
Design of reinforced concrete structures started in the beginning of last century following purely empirical approach. Thereafter came the so called rigorous elastic theory where the levels of stresses in concrete and steel are limited so that stress-deformations are taken to be linear. However, the limit state method, though semi-empirical approach, has been found to be the best for the design of reinforced concrete structures.
Working Stress or Elastic Method
Working stress or Elastic Method is a method used for the reinforced concrete design where concrete is assumed as elastic, steel and concrete act together elastically where the relationship between loads and stresses is linear. This was the traditional method of design not only for reinforced concrete, but also for structural steel and timber design.
Modulus of elasticity of concrete(Ec) is defined as the ratio of the applied stress to the corresponding strain. Not only does it demonstrate the ability of concrete to withstand deformation due to applied stress but also its stiffness.
In other words
Modulus of Elasticity = Stress/Deformation
Modular Ratio is defined as the Ratio between Modulus of Elasticity of Steel and Modulus of Elasticity of Concrete.
It is represented by nation ?m? here. As there is no relative movement between concrete and steel in a reinforced concrete unit, the elongation or contraction of both concrete and steel is equal. As such modular ratio m is proportional to the permissible stresses in steel and concrete which work together.
In other words
Modulus of Elasticity of Steel/Modulus of Elasticity in Concrete
= Stress in steel /stress in concrete = m
Th modulus of elasticity of steel is taken at a constant value 200000 N/mm2 but the modules of elasticity in Concrete is variable and varies with the strength of the particular concrete.
The modular ratio specified in the Indian code of Practise IS 28000/3fc, where fc is maximum permissible compressive stress due to bending in Concrete in Kg./sq.cm
| Grades of Concrete | Modular Ratio |
| M250 = 1:1:2 | M11 |
| M100 = 1 :3:6 | 31 |
| M150 = 1:2:4 | 18.7 |
| M200 = 1:1.5:3 | 13.3 |
According 1978 code value of m is 280/3fc where fc is in N/mm2
When a steel Bar is embedded in the bottom of a concrete beam and the beam if stressed the concrete and the steel is extended and compress equally together provided there is no slip of the bar in the concrete, the deformation in both the materials will be equal. Since stresses are proportional to the respective elastic moduli, the stress in the steel will be ?m? times the stress in the concrete.
Similarly, if a steel bar is embedded in concrete column, then under load the steel and the concrete both must shorten by an equal amount, and since the steel takes ?m? times more stress than the concrete when strained equally, the steel will carry ?m? times more load per unit area than the concrete.
The tensile stress (in the bottom portion of a beam under load) is in design assumed to be carried wholly by the steel, the strength of the concrete in tension being neglected as it will have failed before the steel is fully stressed under the working load; the concrete on the tensile side will always crack (though the crack may not be visible to the naked eye).
Due to inequalities of workmanship and materials and variable conditions during placing and other reasons, strength of the concrete will be found to differ considerably even in adjacent parts of the same structure. Many assumptions are made in reinforced concrete design; therefore, fictitious accuracies are merely a waste of time.
Different Grades of Concrete
Grade of concrete is defined as the minimum strength the concrete must possess after 28 days of construction with proper quality control. Grade of concrete is denoted by prefixing M to the desired strength in MPa. Basically, in this article we will discuss about ordinary concrete and controlled concrete.
Ordinary Concrete
Ordinary Concrete is one of the most commonly used types of concrete. In this type of concrete, the essential constituents are cement, sand and coarse aggregates designed, and mixed with a specified quantity of water.
The ratio of essential constituents may be varied within wide limits. A very commonly used mix design, commonly known as Nominal Mix Design, is 1:2:4.
Controlled Concrete
Controlled concrete is one of the most commonly used types of concrete. In this type of concrete, the essential constituents are cement, sand and coarse aggregates designed, and mixed with a specified quantity of water.
The ratio of essential constituents may be varied within wide limits.
A very commonly used mix design, commonly known as Nominal Mix Design, is 1:2:4.
Conclusion
Good structural analysis and design must be complemented with appropriate reinforcement detailing to ensure that the structure as a whole behaves as it is modelled by the designer. On the other hand, a poorly detailed structure may suffer from unsightly cracks, excessive deflection, or even collapse. Good details and bar arrangements should be practical, buildable, cost-effective, and suitable for their intended use.